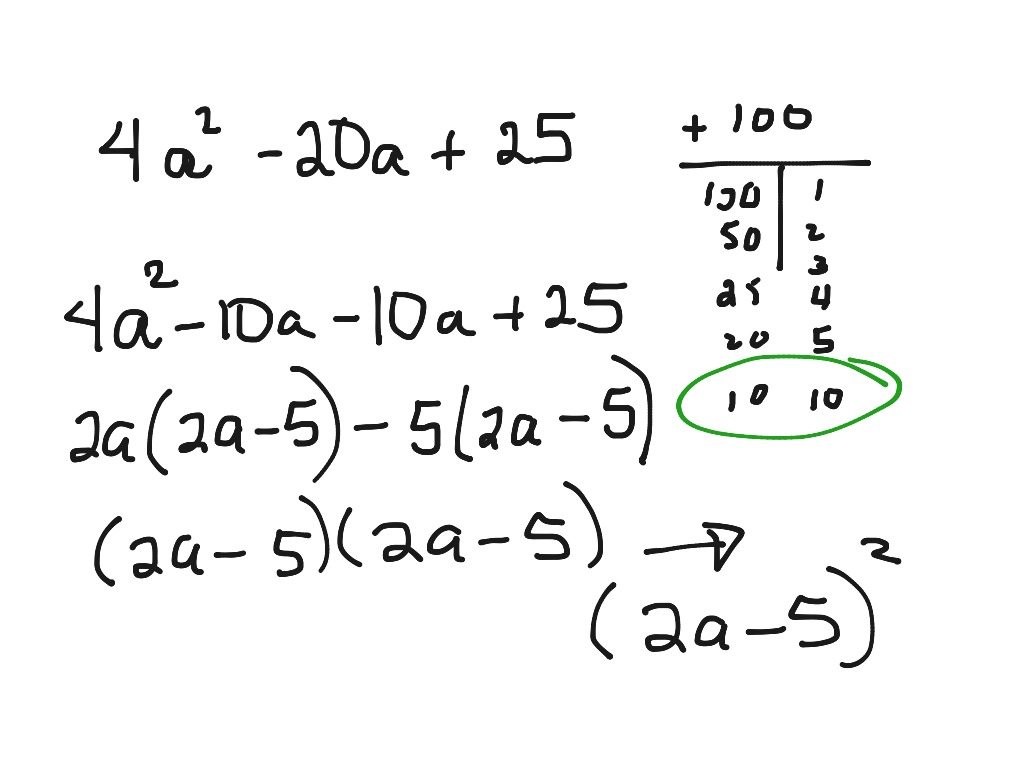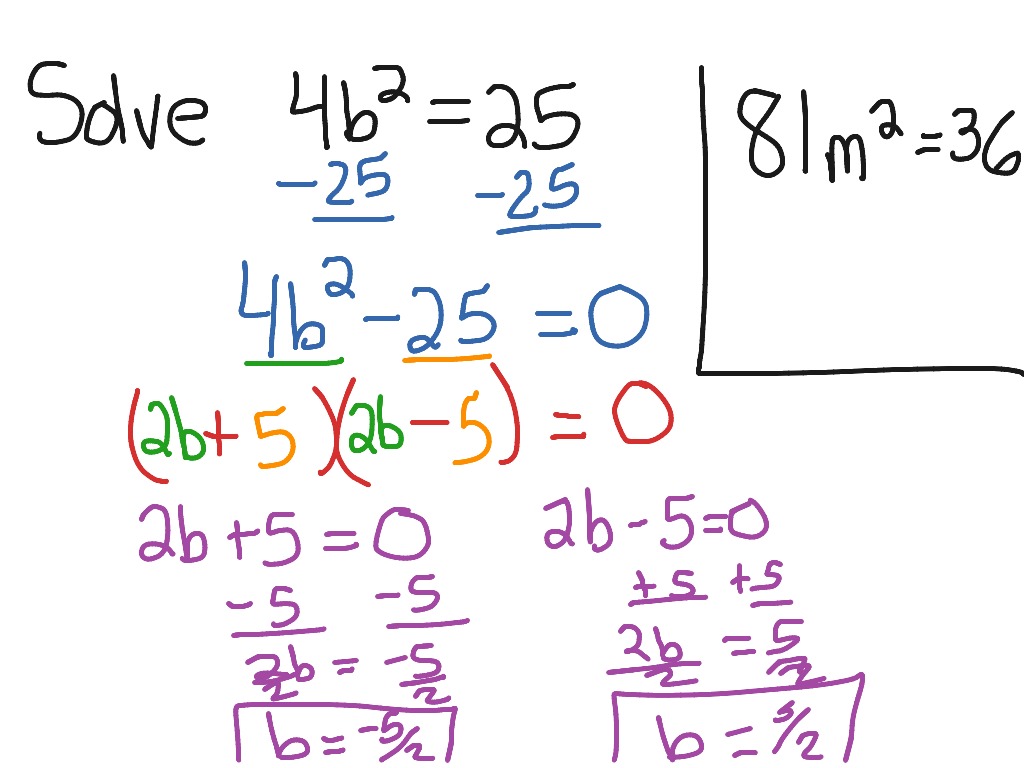What Are Special Products In Math
What Are Special Products In Math - While you can always get. We just developed special product patterns for binomial squares. Mathematicians like to look for patterns that will make their work easier. Applying special products enables us to factorize polynomials. Special products allow us to expand expressions without using the foil method. A good example of this is squaring binomials. In this lesson, we will show various formulas that can be used to find certain binomial products that occur frequently. Recognize and use the appropriate special product pattern. We refer to these commonly. Special products are formulas that allow us to quickly expand certain powers and products of polynomials, and vice versa to.
Special products are formulas that allow us to quickly expand certain powers and products of polynomials, and vice versa to. While you can always get. We refer to these commonly. Recognize and use the appropriate special product pattern. Mathematicians like to look for patterns that will make their work easier. A good example of this is squaring binomials. Applying special products enables us to factorize polynomials. Special products allow us to expand expressions without using the foil method. We just developed special product patterns for binomial squares. In this lesson, we will show various formulas that can be used to find certain binomial products that occur frequently.
Recognize and use the appropriate special product pattern. We just developed special product patterns for binomial squares. Applying special products enables us to factorize polynomials. In this lesson, we will show various formulas that can be used to find certain binomial products that occur frequently. We refer to these commonly. While you can always get. Special products are formulas that allow us to quickly expand certain powers and products of polynomials, and vice versa to. Special products allow us to expand expressions without using the foil method. Mathematicians like to look for patterns that will make their work easier. A good example of this is squaring binomials.
Factoring Special Cases Worksheet Printable Word Searches
While you can always get. We refer to these commonly. A good example of this is squaring binomials. Mathematicians like to look for patterns that will make their work easier. In this lesson, we will show various formulas that can be used to find certain binomial products that occur frequently.
special products Math, Algebra 2 ShowMe
We just developed special product patterns for binomial squares. We refer to these commonly. Special products are formulas that allow us to quickly expand certain powers and products of polynomials, and vice versa to. In this lesson, we will show various formulas that can be used to find certain binomial products that occur frequently. Applying special products enables us to.
Factoring Special Products Difference of Squares Perfect Square
Applying special products enables us to factorize polynomials. Mathematicians like to look for patterns that will make their work easier. Special products are formulas that allow us to quickly expand certain powers and products of polynomials, and vice versa to. Recognize and use the appropriate special product pattern. While you can always get.
MATH GRADE 8 Part A Factoring and Special Products PDF
Special products allow us to expand expressions without using the foil method. We just developed special product patterns for binomial squares. A good example of this is squaring binomials. In this lesson, we will show various formulas that can be used to find certain binomial products that occur frequently. Mathematicians like to look for patterns that will make their work.
Algebra Lesson 73 Special Products of Binomials YouTube
Mathematicians like to look for patterns that will make their work easier. In this lesson, we will show various formulas that can be used to find certain binomial products that occur frequently. We just developed special product patterns for binomial squares. Applying special products enables us to factorize polynomials. Recognize and use the appropriate special product pattern.
Special products Math, Algebra, Simplifying Expressions, Special
We just developed special product patterns for binomial squares. Special products allow us to expand expressions without using the foil method. We refer to these commonly. A good example of this is squaring binomials. While you can always get.
9.7 Factor special Products Math, Algebra, Factoring ShowMe
Mathematicians like to look for patterns that will make their work easier. Special products allow us to expand expressions without using the foil method. Special products are formulas that allow us to quickly expand certain powers and products of polynomials, and vice versa to. We refer to these commonly. We just developed special product patterns for binomial squares.
5 Minute Math Special Products (difference of squares) YouTube
A good example of this is squaring binomials. Applying special products enables us to factorize polynomials. Recognize and use the appropriate special product pattern. In this lesson, we will show various formulas that can be used to find certain binomial products that occur frequently. While you can always get.
Special Products Product of Sum and Difference of Two Terms Part 1
Special products allow us to expand expressions without using the foil method. While you can always get. Recognize and use the appropriate special product pattern. Mathematicians like to look for patterns that will make their work easier. Applying special products enables us to factorize polynomials.
PPT P.3 Polynomials and Special Products PowerPoint Presentation
Recognize and use the appropriate special product pattern. A good example of this is squaring binomials. We refer to these commonly. While you can always get. Mathematicians like to look for patterns that will make their work easier.
Special Products Are Formulas That Allow Us To Quickly Expand Certain Powers And Products Of Polynomials, And Vice Versa To.
While you can always get. Special products allow us to expand expressions without using the foil method. In this lesson, we will show various formulas that can be used to find certain binomial products that occur frequently. Mathematicians like to look for patterns that will make their work easier.
We Refer To These Commonly.
Recognize and use the appropriate special product pattern. A good example of this is squaring binomials. We just developed special product patterns for binomial squares. Applying special products enables us to factorize polynomials.