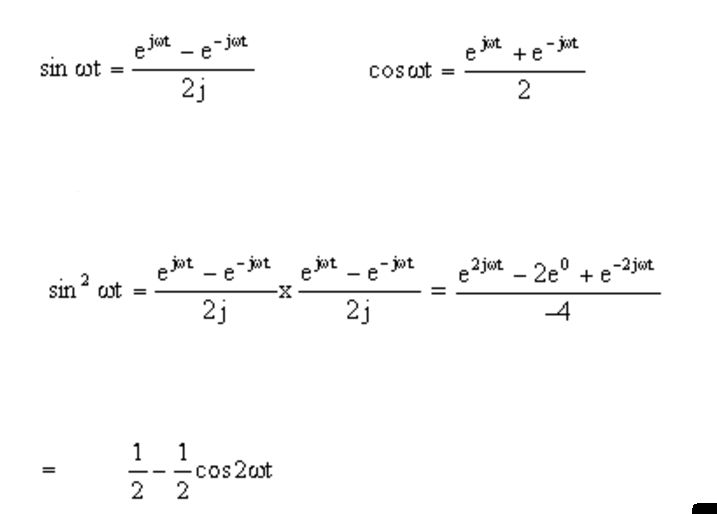
Sin And Cos In Exponential Form
Sin And Cos In Exponential Form - E¡it since we know that cos(t) is even in t and sin(t) is odd in t. We can also express the trig functions in terms of the complex exponentials eit; Technically, you can use the maclaurin series of the exponential function to evaluate sine and cosine at whatever value of. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. These formulas allow us to define sin and cos for complex inputs. The existence of these formulas allows us to solve 2 nd order differential.
Technically, you can use the maclaurin series of the exponential function to evaluate sine and cosine at whatever value of. E¡it since we know that cos(t) is even in t and sin(t) is odd in t. These formulas allow us to define sin and cos for complex inputs. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. The existence of these formulas allows us to solve 2 nd order differential. We can also express the trig functions in terms of the complex exponentials eit;
E¡it since we know that cos(t) is even in t and sin(t) is odd in t. Technically, you can use the maclaurin series of the exponential function to evaluate sine and cosine at whatever value of. The existence of these formulas allows us to solve 2 nd order differential. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. We can also express the trig functions in terms of the complex exponentials eit; These formulas allow us to define sin and cos for complex inputs.
FileSine Cosine Exponential qtl1.svg Wikimedia Commons Math
E¡it since we know that cos(t) is even in t and sin(t) is odd in t. We can also express the trig functions in terms of the complex exponentials eit; These formulas allow us to define sin and cos for complex inputs. Technically, you can use the maclaurin series of the exponential function to evaluate sine and cosine at whatever.
e^x=cos(x)+i sin(x). Where does that exponential form of complex
We can also express the trig functions in terms of the complex exponentials eit; E¡it since we know that cos(t) is even in t and sin(t) is odd in t. These formulas allow us to define sin and cos for complex inputs. Technically, you can use the maclaurin series of the exponential function to evaluate sine and cosine at whatever.
QPSK modulation and generating signals
The existence of these formulas allows us to solve 2 nd order differential. Technically, you can use the maclaurin series of the exponential function to evaluate sine and cosine at whatever value of. We can also express the trig functions in terms of the complex exponentials eit; E¡it since we know that cos(t) is even in t and sin(t) is.
Complex Numbers 4/4 Cos and Sine to Complex Exponential YouTube
From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. These formulas allow us to define sin and cos for complex inputs. The existence of these formulas allows us to solve 2 nd order differential. Technically, you can use the maclaurin series of the exponential function to evaluate sine and cosine.
Expressing Various Complex Numbers in Exponential Form Tim Gan Math
The existence of these formulas allows us to solve 2 nd order differential. We can also express the trig functions in terms of the complex exponentials eit; E¡it since we know that cos(t) is even in t and sin(t) is odd in t. Technically, you can use the maclaurin series of the exponential function to evaluate sine and cosine at.
Exponential Form of Complex Numbers
Technically, you can use the maclaurin series of the exponential function to evaluate sine and cosine at whatever value of. The existence of these formulas allows us to solve 2 nd order differential. These formulas allow us to define sin and cos for complex inputs. From these relations and the properties of exponential multiplication you can painlessly prove all sorts.
Question Video Converting the Product of Complex Numbers in Polar Form
Technically, you can use the maclaurin series of the exponential function to evaluate sine and cosine at whatever value of. E¡it since we know that cos(t) is even in t and sin(t) is odd in t. The existence of these formulas allows us to solve 2 nd order differential. From these relations and the properties of exponential multiplication you can.
A Trigonometric Exponential Equation with Sine and Cosine Math
From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. We can also express the trig functions in terms of the complex exponentials eit; These formulas allow us to define sin and cos for complex inputs. The existence of these formulas allows us to solve 2 nd order differential. E¡it since.
Euler's exponential values of Sine and Cosine Exponential values of
We can also express the trig functions in terms of the complex exponentials eit; These formulas allow us to define sin and cos for complex inputs. E¡it since we know that cos(t) is even in t and sin(t) is odd in t. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities.
Question Video Converting Complex Numbers from Polar to Exponential
The existence of these formulas allows us to solve 2 nd order differential. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. These formulas allow us to define sin and cos for complex inputs. We can also express the trig functions in terms of the complex exponentials eit; Technically, you.
From These Relations And The Properties Of Exponential Multiplication You Can Painlessly Prove All Sorts Of Trigonometric Identities That.
Technically, you can use the maclaurin series of the exponential function to evaluate sine and cosine at whatever value of. E¡it since we know that cos(t) is even in t and sin(t) is odd in t. We can also express the trig functions in terms of the complex exponentials eit; The existence of these formulas allows us to solve 2 nd order differential.