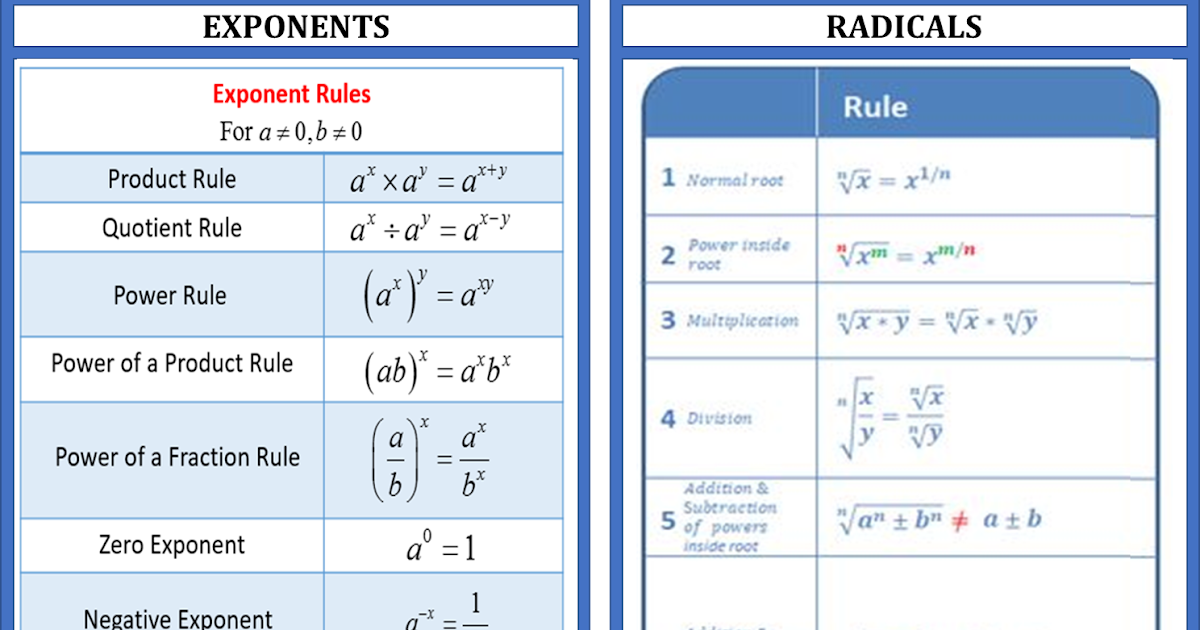
Rules Of Radicals In Math
Rules Of Radicals In Math - To simplify my job a. Roots (or radicals) are the opposite operation of applying exponents; The rules of radicals™ radicals, like literally any other operation, have some properties and conditions for existence. Radical expressions can be rewritten using exponents, so the rules below are a subset of. We will also give the properties of radicals and. Algebra rules for nth roots are listed below. In this section we will define radical notation and relate radicals to rational exponents. We can undo a power with a radical, and we can undo a radical with.
Roots (or radicals) are the opposite operation of applying exponents; Algebra rules for nth roots are listed below. We can undo a power with a radical, and we can undo a radical with. The rules of radicals™ radicals, like literally any other operation, have some properties and conditions for existence. In this section we will define radical notation and relate radicals to rational exponents. We will also give the properties of radicals and. Radical expressions can be rewritten using exponents, so the rules below are a subset of. To simplify my job a.
In this section we will define radical notation and relate radicals to rational exponents. Roots (or radicals) are the opposite operation of applying exponents; We can undo a power with a radical, and we can undo a radical with. We will also give the properties of radicals and. Algebra rules for nth roots are listed below. The rules of radicals™ radicals, like literally any other operation, have some properties and conditions for existence. To simplify my job a. Radical expressions can be rewritten using exponents, so the rules below are a subset of.
What are radicals in maths
We can undo a power with a radical, and we can undo a radical with. Algebra rules for nth roots are listed below. Radical expressions can be rewritten using exponents, so the rules below are a subset of. We will also give the properties of radicals and. Roots (or radicals) are the opposite operation of applying exponents;
1.1 Rules for Exponents and Radicals
Roots (or radicals) are the opposite operation of applying exponents; Algebra rules for nth roots are listed below. In this section we will define radical notation and relate radicals to rational exponents. We will also give the properties of radicals and. To simplify my job a.
Exponents and Radicals Studying math, Math methods, Exponent rules
The rules of radicals™ radicals, like literally any other operation, have some properties and conditions for existence. To simplify my job a. We will also give the properties of radicals and. We can undo a power with a radical, and we can undo a radical with. Radical expressions can be rewritten using exponents, so the rules below are a subset.
Algebra I Help Simplifying Radicals II Quotient Rule for Radicals
Algebra rules for nth roots are listed below. The rules of radicals™ radicals, like literally any other operation, have some properties and conditions for existence. In this section we will define radical notation and relate radicals to rational exponents. Radical expressions can be rewritten using exponents, so the rules below are a subset of. We can undo a power with.
Algebra Laws of Radicals YouTube
To simplify my job a. The rules of radicals™ radicals, like literally any other operation, have some properties and conditions for existence. We will also give the properties of radicals and. Radical expressions can be rewritten using exponents, so the rules below are a subset of. Roots (or radicals) are the opposite operation of applying exponents;
How To Simplify Radicals Simplifying Square Roots Algebra 2 Review
We can undo a power with a radical, and we can undo a radical with. We will also give the properties of radicals and. Radical expressions can be rewritten using exponents, so the rules below are a subset of. In this section we will define radical notation and relate radicals to rational exponents. To simplify my job a.
PPT Properties of Radical Expressions PowerPoint Presentation, free
Roots (or radicals) are the opposite operation of applying exponents; We can undo a power with a radical, and we can undo a radical with. We will also give the properties of radicals and. To simplify my job a. In this section we will define radical notation and relate radicals to rational exponents.
Rules for Radicals & Rational Exponents Radicals math, Math methods
In this section we will define radical notation and relate radicals to rational exponents. The rules of radicals™ radicals, like literally any other operation, have some properties and conditions for existence. We can undo a power with a radical, and we can undo a radical with. Radical expressions can be rewritten using exponents, so the rules below are a subset.
Quadratic Equation Discriminant Rules avsfashionproduct
We can undo a power with a radical, and we can undo a radical with. Radical expressions can be rewritten using exponents, so the rules below are a subset of. To simplify my job a. The rules of radicals™ radicals, like literally any other operation, have some properties and conditions for existence. Algebra rules for nth roots are listed below.
Pin by Om Prakash on Teach them well Radicals math, Radical equations
The rules of radicals™ radicals, like literally any other operation, have some properties and conditions for existence. Algebra rules for nth roots are listed below. To simplify my job a. We will also give the properties of radicals and. Radical expressions can be rewritten using exponents, so the rules below are a subset of.
To Simplify My Job A.
Radical expressions can be rewritten using exponents, so the rules below are a subset of. Algebra rules for nth roots are listed below. In this section we will define radical notation and relate radicals to rational exponents. Roots (or radicals) are the opposite operation of applying exponents;
We Can Undo A Power With A Radical, And We Can Undo A Radical With.
We will also give the properties of radicals and. The rules of radicals™ radicals, like literally any other operation, have some properties and conditions for existence.